Les réseaux de neurones
A) les réseaux de neurones biologique
Ce qui rend les neurones de notre cerveau uniques c'est aussi leur assemblage particulier qui leur permet de réaliser des calculs et de mémoriser des informations.
On peut se demander comment ces cent milliards de neurones sont à l'origine de la fonction cérébrale. Mais il n'est pas facile de répondre à cette question en étudiant les réseaux de neurones lorsque l'on sait que chaque neurone est relié à 10 milles de ses semblables.
Les neurophysiciens se sont demandés si des problèmes analogues n'avaient pas déjà été surmontés et ils ont trouvé que des chercheurs avaient eu le même problème pour étudier les comportements des systèmes macroscopiques avant de découvrir l’entropie. Cette grandeur mathématique est un des paramètres qui décrit l'état d'un système. Et lorsqu'elle varie, elle ne tend qu'à croître.
De la même façon Hopfield, professeur au département de biologie moléculaire à l'Université de Princeton, a défini une grandeur mathématique qu'il a appelée énergie calculatoire. Il a proposé que l'énergie calculatoire d'un neurone devait toujours tendre vers sa valeur la plus basse. Cela n'a pas permis de percer tous les mystères mais cette nouvelle notion a par exemple une application pour comprendre la mémoire d'un réseau.
Le calcul collectif
Comme je l'ai dit un peu plus haut les neurones ont deux fonctions principales et la première est de réaliser des calculs. Comme pour les ordinateurs ou pour les robots une action résulte d'un calcul mais les ordinateurs et les réseaux de neurones ne calculent pas du tout de la même façon. Comme c'est un peu difficile à expliquer voici un exemple concret:
4 personnes doivent ranger une bibliothèque avec 4 domaines d'ouvrages différents en y passant le moins de temps possible. Chaque personne ne peut s'occuper que d'un domaine et on doit trouver le meilleur choix assistant/matière.
|
|
Marcel |
Victor |
Sylvie |
Axelle |
|
Sciences |
10 livres par heures |
4 livres par heures |
4 livres par heures |
6 livres par heures |
|
Histoire |
8 livres par heures |
4 livres par heures |
1 livres par heures |
1 livres par heures |
|
Art |
1 livres par heures |
8 livres par heures |
9 livres par heures |
6 livres par heures |
|
Romans |
5 livres par heures |
4 livres par heures |
7 livres par heures |
1 livres par heures |
Il y a en tout 24 possibilités.
Un ordinateur les examine l’une après l’autre; pour chacune d’entre elles, il calcule le temps qu'il faudrait pour que tous les livres soit rangés, puis il donne la meilleure solution.
Une machine de Hopfield, qui a été créée par le physicien du même nom, sur le modèle des réseaux de neurones, est formée de 16 modules interconnectés. Il y a un module par appariement: Marcel/science; Marcel/Histoire...(voir l'image ci- dessous)
Chaque module est relié à 6 autres de ses homologues:
Plus un assistant est doué dans une matière plus sa désignation pour ranger celle-ci doit être prise en considération. Cela se traduit dans l'architecture de la machine avec des connections inhibitrices.
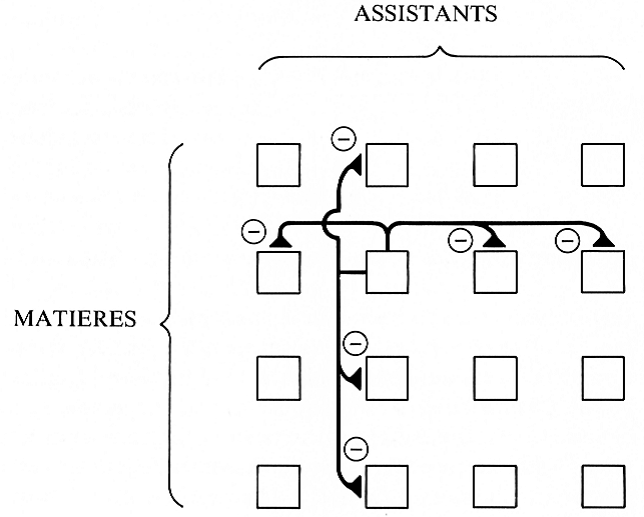
Toutes ces connexions reflètent bien la nature du problème. Certes Marcel est le meilleur en science mais ce n'est pas pour cela qu'il doit être désigné à ce poste, cela dépend aussi de ses collègues. C’est cela le calcul collectif.
La mémorisation
La mémoire d'un neurone
L'autre grande fonction des neurones est d'apprendre.
Tout au long de notre existence nos cellules se divisent en cellules filles, qui sont des clones de la cellule mère.
Ce n'est pas le cas des neurones, ils sont immuables, une femme de 50 ans possède les mêmes neurones qu'à sa naissance. Cependant si les neurones sont immuables, les synapses, elles ne le sont pas. Elles peuvent devenir obsolètes et disparaître, elles peuvent aussi se créer. Ou alors leur aptitude à exciter ou à inhiber peut varier.
Prenons par exemple un escargot de mer. Lorsque l'on touche légèrement son siphon, on déclenche une contraction des muscles de ses branchies. Lorsque la simulation est suivie immédiatement d'un choc électrique sur la queue de l'animal, le réflex de retrait des branchies est augmenté. Après avoir habitué l'animal à cette association, on enlève le choc électrique et on recommence à toucher le siphon. La réaction des branchies reste extrêmement vive. Le mollusque a retenu que la stimulation tactile entraînait une stimulation électrique.
Regardons le circuit impliqué dans ce réflexe. La fibre dendrite du neurone sensitif innerve le siphon. L'axone du neurone moteur innerve les muscles des branchies .Et l'axone du neurone sensitif est relié au neurone moteur par une de ses synapses. Voilà la situation de départ.
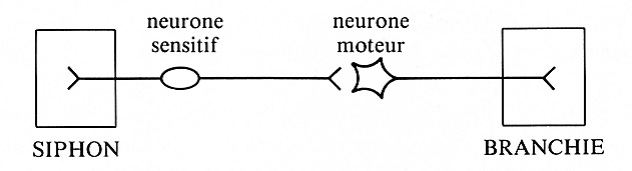
Lorsque l'on touche le siphon de l'escargot de mer, une multitude de potentiels d'action sont conduits du neurone sensitif jusqu'à la synapse où ils libèrent des médiateurs chimiques qui excitent le neurone moteur qui, à son tour déclenche la contraction musculaire et donc la rétraction des branchies.
Maintenant si l'efficacité synaptique est doublée, le toucher du siphon déclenchera mêmes multitudes de potentiels d'actions dans la fibre sensitive mais ceux-ci excitent les neurones moteurs deux fois plus fort et la contraction des branchies est elle aussi deux fois plus forte.
C'est ce qu'il se passe au cours de l'apprentissage.
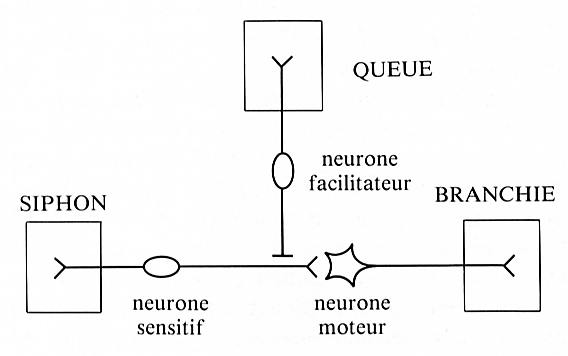
Pour comprendre le mécanisme qui a déclenché cette modification il faut rajouter un neurone facilitateur au schéma. Sa fibre dendrite innerve la queue de l'animal et dont l'extrémité axonal vient en contact synaptique avec l'extrémité de l'axone du neurone sensitif. Sa synapse est particulière, elle n'envoie pas des neurotransmetteurs lorsqu'elle est excitée mais elle provoque à l'extrémité de l'axone du neurone sensitif la fabrication de molécules d'une substance appelée AMP cyclique.
Cela a pour effet de permettre à la synapse de libérer une plus grande quantité de médiateurs chimiques, donc d'exciter davantage le neurone moteur.La mémoire d'un neurone doit reposer sur des modifications chimiques car elles durent dans le temps.
La mémoire d'un réseau de neurones
Vous venez de voir ce qu'est la mémoire d'un neurone. Mais ce qui est important avec les neurones, ce n'est pas leur comportement individuel mais leur comportement collectif. Or pour suivre l'état d'un réseau de neurones, il faut suivre son évolution à travers la variable de Hopfield.
Pour schématiser cela, voici un bloc en relief composé de 25 droites s’entrecroisant perpendiculairement avec 25 autres droites. Chaque intersection représente un état possible et l'énergie calculatoire de ces états est représentée par la hauteur du bloc.
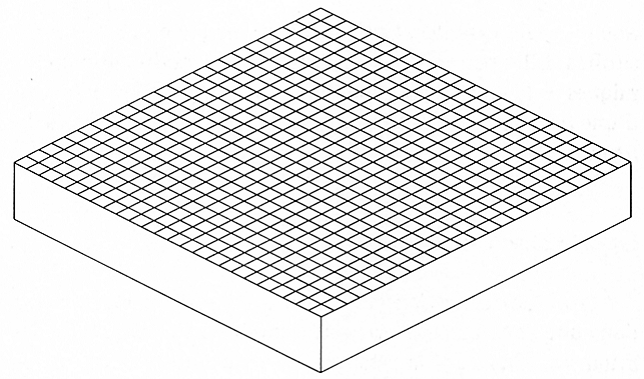
Au départ la mémoire du réseau est vide, toutes les synapses ont la même efficacité.
Maintenant imprimons un souvenir
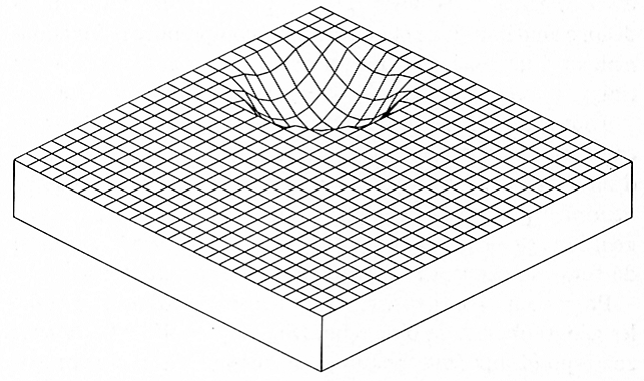
Un trou se creuse dans les blocs mais ses pentes ne sont pas très raides. L’énergie calculatoire n'a donc pas diminué, qu’à un seul endroit, elle a aussi diminué dans les états voisins.
Maintenant inscrivons un autre souvenir
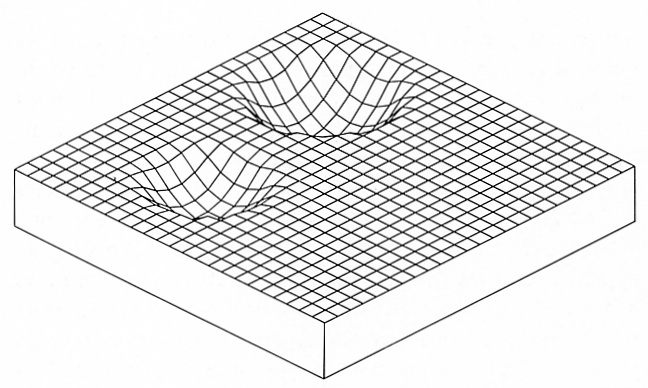
B) Perceptron et réseau de neurones artificiels
Le perceptron
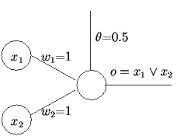
Un perceptron linéaire à seuil prend en entrée n valeurs x1 ....xn et calcule une sortie o. Un perceptron est défini par la donnée de n+1 constantes; il y a les coefficients synaptiques w1,....wn et le seuil 0
La sortie o est calculée par la formule:
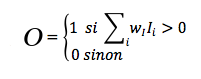
Un perceptron c'est donc ceci:
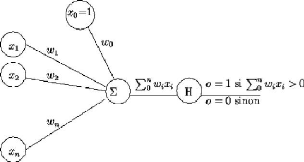
Un perceptron est donc la modélisation mathématique d’un neurone biologique.
Les entrées correspondent aux dendrites chez les neurones biologiques, les valeurs d'entrées sont couramment {0,1} ou {-1 ; 1}
x0 représente le seuil de déclanchement, chez un neurone biologique il est de -30 mV ici c'est une constante. Les coefficients synaptiques eux permettent de représenter les neurones inhibiteurs et excitateurs ainsi que les différentes efficacités des neurones.
Le perceptron ne réalise ainsi qu’une somme pondérée. Grâce à lui, on peut facilement calculer le OU d’une fonction Booléenne.
Fonction Booléenne
Une fonction booléenne est une fonction prenant en entrée une liste de bit (0 ; 1) et donnant en sortie un unique bit.
Bit : unité la plus simple dans un système de numération, ne pouvant prendre que deux valeurs désignées le plus souvent par {0 ; 1} ou {-1 ; 1}.
Les fonctions booléennes font partie de l’algèbre de Boole :
On appelle B l’ensemble constitué de deux éléments appelés valeurs de vérités : {Vrai ; Faux} aussi noté B= {0 ; 1} ou {-1 ; 1}.
Sur cet ensemble on définit deux lois ET et OU.
Conjonction (loi ET)
Elle est définie de manière suivante a ET b est Vrai si et seulement si a est Vrai et b est Vrai. Elle est notée « . »
|
b/a |
0 |
1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
Disjonction (loi du OU)
Elle est définie de manière suivante a OU b est Vrai si et seulement si a est Vrai ou B est Vrai (ou les deux sont vraies)
Cette loi est notée « + »
|
b/a |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
1 |
Un perceptron qui calcule le OU logique:
L’algorithme d’apprentissage par correction d’erreur
C’est un algorithme qui permet de faire mémoriser des choses à un perceptron.
Pour expliquer cette notion prenons un exemple : l’ordinateur doit apprendre à reconnaître si les chiffres sont pairs ou impairs, on considère un échantillon de 10 chiffres :
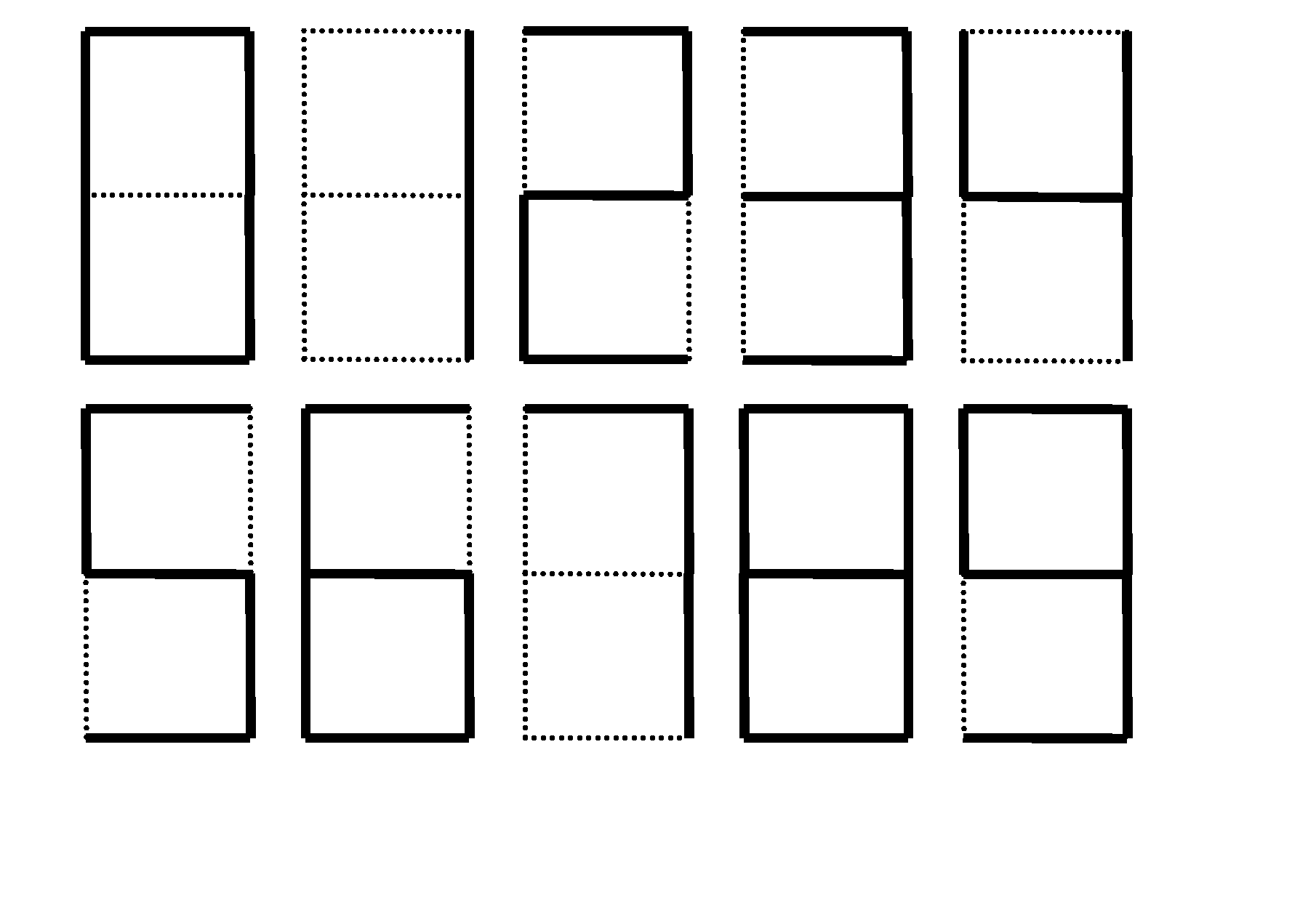
Pour que l’ordinateur puisse les comprendre on lui traduit :

Pour commencer on initialise les poids du perceptron (w1…wn) à des valeurs quelconques. A chaque fois que l’on présente un nouvel exemple, on ajuste le poids suivant si le perceptron est correctement classé ou non. Il s’arrête lorsque tous les éléments lui ont été présentés sans qu’il ait eu besoin de modifier un poids.
Voici l’algorithme :
c est la sortie attendue,o est la sortie calculée et S est l’ensemble des exemples
Répéter
Prendre un exemple dans S
Si wi xi > seuil o=1
Sinon o=0
Pour i de 0 à n
Wi prend la valeur wi +(c-o) xi
Fin pour
Fin répéter
Voilà comment on peut apprendre des choses à un neurone artificiel.
Les réseaux de neurones artificiels
Comme pour les neurones biologiques, les neurones artificiels peuvent être organisés en réseaux.
Il en existe deux types, les réseaux de neurones bouclés et les réseaux de neurones non bouclés.
Nous verrons seulement les réseaux de neurones non bouclés.
Les réseaux de neurones non bouclés :
Un réseau de neurone non bouclé est représenté graphiquement par un ensemble de neurones connectés entre eux, l’information circulant des entrées vers la ou les sortie(s) sans retour en arrière.
.jpg)
Ceci est un perceptron multi-couches.Il est défini grâce à une architecture vérifiant les propriétés suivantes : La première couche est composée par n cellules d’entrées, qui correspondent aux n variables. Les couches C1….Cq-1 sont les couches dites cachées et Cq est la couche de sortie(s). Les entrées d’une cellule d’une couche i (i≥1) sont toutes les cellules de la couche précédente et aucune autre cellule.
Ce type de réseau peut par exemple effectuer des classes de classification ou pour calculer le XOR d’une fonction booléenne.
Le XOR d’une fonction booléenne (ou OU exclusif) est défini de manière suivante a est Vrai ou b est Vrai mais pas les deux.
|
b/a |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
Perceptron calculant le XOR d'une fonction booléenne:
.png)
